Golden Rectangle

A golden rectangle is one whose side lengths are in the golden ratio, or approximately 1:1.618.

A distinctive feature of this shape is that when a square section is removed, the remainder is another golden rectangle; that is, with the same aspect ratio as the first. Square removal can be repeated infinitely, in which case corresponding corners of the squares form an infinite sequence of points on the golden spiral, the unique logarithmic spiral with this property.

  

A golden rectangle with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship

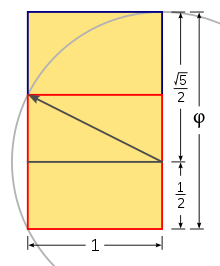
A golden rectangle can be constructed with only straightedge and compass by this technique:

1. Construct a simple square.  
2. Draw a line from the midpoint of one side of the square to an opposite corner.
3. Use that line as the radius to draw an arc that defines the height of the rectangle.
4. Complete the golden rectangle.
5. 
   

   A method to construct a golden rectangle. The square is outlined in red. The resulting dimensions are in the golden ratio.

   
   

   The Golden Mean (or Golden Section), represented by the Greek letter phi, is one of those mysterious natural numbers, like e or pi, that seem to arise out of the basic structure of our cosmos. Unlike those abstract numbers, however, phi appears clearly and regularly in the realm of things that grow and unfold in steps, and that includes living things.
   The decimal representation of phi is 1.6180339887499... . 

   THIS IS ALSO CALLED  "THE DIVINE PROPORTION"

   

   
   

   In philosophy, especially that of Aristotle, the golden mean is the desirable middle between two extremes, one of excess and the other of deficiency. For example courage, a virtue, if taken to excess would manifest as recklessness and if deficient as cowardice.

   To the Greek mentality, it was an attribute of beauty. Both ancients and moderns realized that there is a close association in mathematics between beauty and truth. The poet John Keats, in his Ode on a Grecian Urn, put it this way:

   "Beauty is truth, truth beauty," -- that is all..Ye know on earth, and all ye need to know.

   The Greeks believed there to be three 'ingredients' to beauty: symmetry, proportion, and harmony. This triad of principles infused their life. They were very much attuned to beauty as an object of love and something that was to be imitated and reproduced in their lives, architecture, education (Paideia) and politics. They judged life by this mentality.

   In Chinese philosophy, a similar concept, Doctrine of the Mean, was propounded by Confucius; Buddhist philosophy also includes the concept of the middle way.
   
   The Divine Proportion was closely studied by the Greek sculptor, Phidias, and as a result, it took on the name of Phi. Also referred to as the Golden Mean, the Magic Ratio, the Fibonacci Series, etc., Phi can be found throughout the universe; from the spirals of galaxies to the spiral of a Nautilus seashell; from the harmony of music to the beauty in art. A botanist will find it in the growth patterns of flowers and plants, while the zoologist sees it in the breeding of rabbits. The entomologist views it in the genealogy of a bee, and the physicist observes it in the behavior of light and atoms. A Wall Street analyst can find it in the rising and falling patterns of a market, while the mathematician uncovers it in the examination of the pentagram.